任意两个要素间的距离,依据它们之间的最短间距计算,也就是两者相互靠近的最近距离。这一逻辑适用于所有计算距离的地理处理工具,例如近邻分析、生成邻近表、点距离以及带有 CLOSEST 匹配选项的空间连接工具。
1、 距离计算应考虑要素的几何类型和坐标系等因素。以下是确定距离计算方法的三条基本规则。
2、 两点间的距离为连接这两点的直线长度。
3、 点到直线的距离,指该点与直线上垂足或最近折点间的长度。
4、 折线间的距离由线段折点决定。
5、 下图展示两点距离,以及邻域分析工具涉及的其他关键要素。

6、 利用生成邻近表和点距离工具,把注释中的关键字(IN_FID、NEAR_DIST、NEAR_FID、NEAR_X、NEAR_Y及NEAR_ANGLE)加入输出结果。同时,在执行近邻分析工具时,将这些关键字添加到输入要素类中。
7、 多点对多点
8、 计算多点间距离的特殊情况时,依据规则1,可测量输入多点要素中每个点到邻近多点要素各点的距离,其中最短距离即为两者之间的距离。
9、 此外,若某多点要素的一点位于另一多点要素的某点之上,则二者距离为零,此规则适用于所有多部分要素。
10、 在 ArcGIS 中,线要素被称为折线,线与折线可互换使用。折线是由多个有序点(称为折点)组成的集合,其中vertex是vertice的单数形式。一条折线可以包含任意数量的折点,而由两个折点构成的线称为线段,这两个折点也被称为端点。
11、 同样,面是被一条或多条折线界定的封闭区域。
12、 点到线段的最短距离为垂线,若垂足不在线段上,则取点到线段两端点较近的距离作为最短距离。
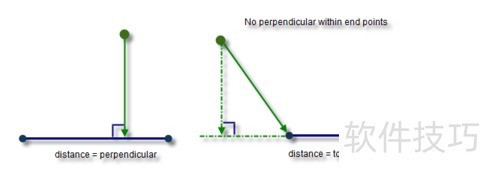
13、 点至折线距离
14、 若折线仅含一条线段,可依规则2计算出该距离。
15、 折线若含多段(常见情形),先找距点最近的线段,再按规则2计算距离。
16、 点到面
17、 面是有序线段集合围成的封闭区域,计算点到面的距离,先确定最近的线段,再按规则2求出距离。
18、 点在面外时距离为正,否则为零。

19、 上图中,点2和点3到平面距离为零,点1和点4到平面的距离为正值。
20、 对于两条非点状要素,例如线段:
21、 根据规则1和规则2,计算输入线段各端点与相邻线段之间的距离值。
22、 计算邻近线段各端点与输入线段的距离。
23、 两条线段的距离为两个距离值中较小的一个。
24、 线与线的交汇
25、 最简单的情况是每个折线要素仅含一条线段。下图展示了从折点 C 向由折点 AB 确定的线段所作垂线 CX。同样可计算折点 D 到该线段的垂线,但其距离大于 CX。因此,CX 为线段 CD 和 AB 间的最短距离。
26、 由于无法从转折点 A 或 B 向线段 CD 作垂线,需计算转折点 A 或 B 到点 C 的距离。最终得出,AC 为线段 AB 至线段 CD 的最短距离。
27、 在计算的两个距离(AC和CX)里,CX为折点到线段的最短距离,故它是两线段间的最短距离。
28、 若两条折线均含多条线段,先确定最近的两线段,然后依据规则3计算其距离。
29、 线条变平面
30、 计算折线与面的距离时,需确定最近的两线段,其中一线段属于折线,另一线段来自面边界的构成线段。依据规则3中的方法,计算这两线段之间的距离。

31、 计算相邻角度
32、 任意两种要素类型间,以两最近点绘制连线,计算距离。该线与水平轴的夹角称为邻近角。
33、 逆时针测量角,该角度位于0到180度之间。

34、 顺时针测量角度,范围在0到-180度之间。

35、 概要
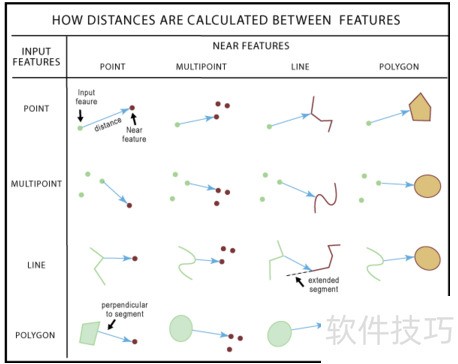
36、 下图展示了不同要素类型间距离的计算方法,以及依据前述内容确定最近位置的方式,未涵盖所有可能组合。