1、 null
2、 标准差与T统计量并无直接关联,二者属于不同类型的统计概念,分别用于衡量数据变异程度和检验统计假设。
3、 标准差用于衡量数据集的离散程度,即便两组数据的平均值相同,其标准差也可能存在差异。
4、 T统计量适用于小样本情况下,对正态分布且方差未知的总体均值进行估计。
5、 标准差与T统计量在定义、计算方式和应用场景上存在三点差异。
6、 意义不同:前者指……,后者指……
7、 标准差是方差的平方根,因方差为数据平方值,与原数据差异较大,不易直观理解,通过开方还原量纲,使结果更贴近原始数据,便于衡量离散程度。
8、 在统计学中,样本均差通常除以自由度(n-1),表示数据可自由变动的数量。当已选定n-1个值时,最后一个值被固定,无法再自由选择,因此自由度为n-1。
9、 t统计量的分布形态由自由度df决定。自由度越小,t分布曲线越平坦,中央区域越低,两侧尾部越高;自由度越大,曲线越趋近于标准正态分布。当自由度趋于无穷大时,t分布完全等同于标准正态分布。因此,t分布随着样本容量增加逐渐逼近正态分布,体现了小样本条件下对总体参数推断的适应性与稳健性。
10、 特征不同:两者各有特点
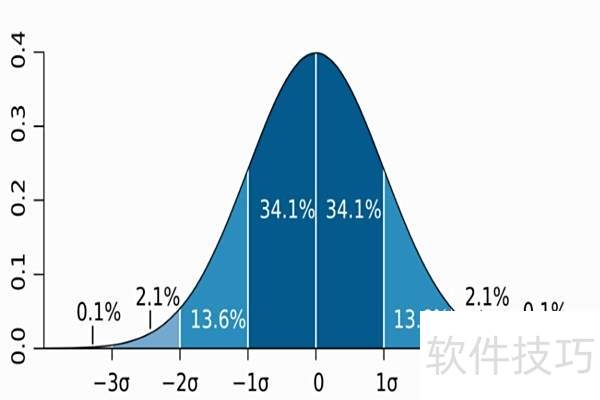
11、 标准差反映数据与平均值的偏离程度,常用M±SD表示,体现观测值与均值的距离。其数值受极端值影响明显,标准差越小,说明数据分布越集中;反之,标准差越大,则表明数据越分散,波动性越强。它是衡量数据离散程度的重要指标。
12、 t分布呈以0为中心、左右对称的单峰形态,属于一族曲线,其形状随样本量n决定的自由度df而变化。自由度越小,曲线越平坦宽缓;自由度越大,曲线越陡峭,形态越趋近于标准正态分布。随着自由度不断增大,t分布逐渐逼近标准正态分布,二者在自由度较高时差异极小。
13、 应用领域不同
14、 标准差是统计学中衡量数据偏离平均值程度的指标,常用于分析价格变动的剧烈程度。当标准差较大时,表明数据波动范围广,价格起伏明显;在金融市场中,这意味着股票等资产的价格波动性较强,风险相对更高。
15、 T统计量是数理统计中的重要理论分布,为多种统计方法提供理论支撑。正态分布由均值μ和标准差σ两个参数决定,分别影响其位置与形状特征。
16、 t分布是小样本统计推断的重要工具。
17、 标准差衡量数据偏离平均值的程度。














