介绍五种经典算法的简明经验。
1、 河内塔谜题
2、 河内塔问题由法国数学家爱德华·卢卡斯于1883年提出,据称其灵感源自泰国流传的一个古老传说。虽然名为河内,实为越战时期北越的首都,即今日的胡志明市。传说在创世之初,印度古城贝拿勒斯有一座神圣的塔庙,庙中有三根钻石柱支撑着一组金盘。最初,神将64个大小不一的金盘按自上而下由小到大的顺序叠放在第一根柱子上。神命令僧侣们将全部金盘从第一根柱子移动至第三根柱子,移动过程中必须遵守一个规则:任何时候都不能将较大的盘子置于较小的盘子之上。僧侣们日复一日,每天仅能移动一个盘子。传说当所有64个金盘成功移完之日,这座塔便会崩塌,世界也将随之终结。这一谜题不仅蕴含深刻的数学原理,更因其背后神秘的传说而广为流传,成为递归思想与算法设计中的经典范例。
3、 方法如下:
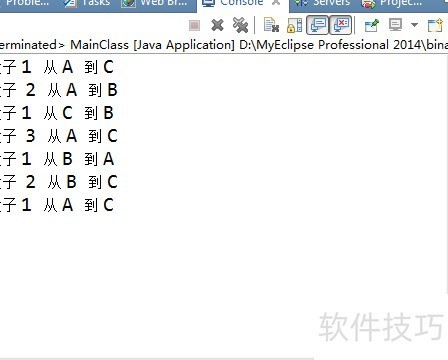
4、 若将三根柱子分别标记为A、B、C,目标是将所有盘子从A移动到C。当只有一个盘子时,直接将其由A移至C即可;若有两个盘子,则借助B作为中转柱进行移动。当盘子数量超过两个时,可将最底层以上的盘子视为一个整体,每次只需处理上方两个盘子的移动,即完成A到B、A到C、B到C三个基本步骤。被暂时忽略的部分则通过递归方式逐步分解处理。实际上,移动n个盘子所需的总步数为2的n次方减1。以64个盘子为例,所需移动次数高达约1.8×10??次。假设每秒移动一次,不中断地进行,也需耗费大约5850亿年才能完成整个过程。
5、 以下示例展示了Java语言实现河内塔问题的过程。
6、 }
7、 将盘子1从起始位置移动到目标位置,并输出移动过程。
8、 输出提示信息:将编号为 topN 的盘子从起始位置 from 移动到目标位置 to,并显示具体移动步骤。
9、 }
10、 }
11、 }
12、 运行效果所示
13、 斐波那契数列
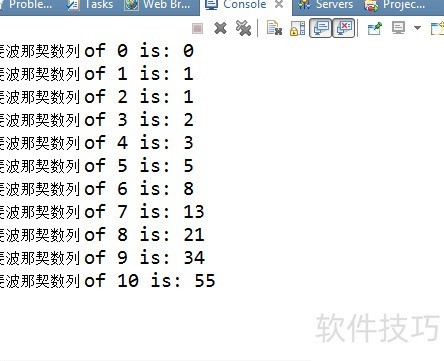
14、 斐波那契数列是一组从0和1开始,之后每一项都等于前两项之和的数列。其序列为:0、1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987、1597、2584、4181、6765、10946、17711、28657、46368……该数列在自然界与数学中广泛存在,展现出独特的规律性与美感。
15、 注意:第0项为0,第1项为首个1。
16、 数列从第三项起,每项为前两项之和。
17、 以下示例展示了Java中斐波那契数列的编程实现方法。
18、 }
19、 输出第 counter 个斐波那契数列的值为:fibonacci(counter)。
20、 }
21、 }
22、 }
23、 运行效果所示
24、 帕斯卡三角形
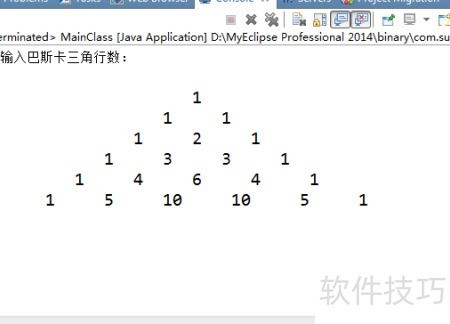
25、 帕斯卡三角形中的每个数字实际上对应一个组合数nCr,其中n代表行数,r代表列数,因此该三角形本质上反映了组合运算的规律。
26、 以下示例展示了Java中帕斯卡三角形的实现方法。
27、 请输入要生成的帕斯卡三角形的行数:
28、 }
29、 }
30、 }
31、 }
32、 }
33、 }
34、 }
35、 }
36、 }
37、 运行效果所示
38、 三色棋局
39、 问题描述:
40、 问题最初由荷兰计算机科学家E.W. Dijkstra提出,他称之为荷兰国旗问题,因其国籍而得名,后来多数人则习惯称为三色旗问题。设想一条绳子上悬挂着红、白、蓝三种颜色的旗子,初始时排列无序。目标是将这些旗子重新排序,使得所有蓝色旗子在前,白色居中,红色在后,形成统一的顺序。整个过程只能在绳子上进行操作,且每次仅允许交换两个旗子的位置。要求设计一种方法,使完成排序所需的交换次数尽可能少,从而达到最优效率。这一问题不仅具有直观的视觉模型,也常被用于算法教学中,体现数组分区与排序思想的精妙结合。
41、 解法
42、 在一条绳子上移动相当于程序中仅用一个数组而不借助其他辅助数组。解决方法类似移动旗帜:从绳子一端开始,蓝色旗子向前移,白色保持居中,红色则向后移。要使移动次数最少,需掌握一定技巧,合理安排交换顺序以提升效率。
43、 以下示例展示了Java语言实现的三色棋程序。
44、 }
45、 }
46、 }
47、 }
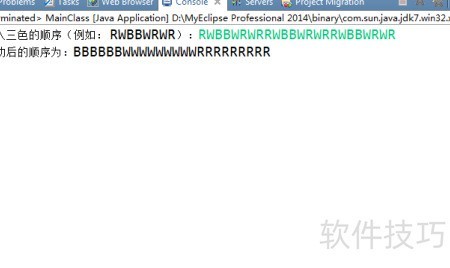
48、 请输入三色排列顺序(如:RWBBWRWR):
49、 打印移动后的新顺序结果:flags。
50、 }
51、 }
52、 运行效果所示
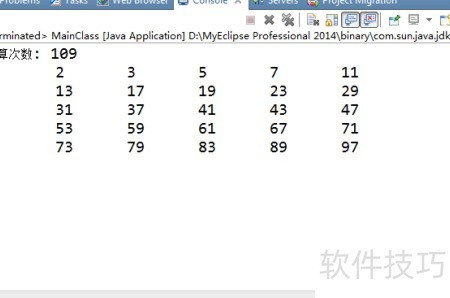
53、 埃拉托斯特尼筛法用于筛选质数。
54、 说明:
55、 只能被1和自身整除的自然数称为质数。寻找质数虽简单,但高效计算始终是数学与编程领域的重要课题。埃拉托斯特尼筛法是一种经典算法,通过逐步筛选排除合数,从而快速找出一定范围内的所有质数,至今仍被广泛应用。
56、 解法:
57、 可通过循环判断一个数是否能被小于它的数整除来确定质数,但为提升效率,需优化循环次数。可采用筛选法,如埃拉托斯特尼筛法,快速找出小于N的所有质数,显著减少重复计算。
58、 判断一个数N是否为质数时,只需检查从2到√N之间的所有整数即可。因为若N存在大于√N的因数,则必然对应一个小于√N的因数,先前已可被检测到。为避免程序中开方运算带来的精度误差,通常采用循环变量i满足i×i ≤ N作为判断条件,既保证准确性,又提升运行效率,是一种更稳定高效的实现方式。
59、 假设有个筛子装着从1到N的数字,比如:
60、 从4开始,以2为步长依次筛选,去除所有2的倍数,保留奇数:3、5、7、9、11、13、15、17、19、21……直至N,初步筛去偶数部分,留下待进一步判断的数列。
61、 从9开始,以3为步长筛选3的倍数并剔除,保留非3倍数的数,如2、3、5、7、11、13、17、19……直至N。
62、 用5进行筛选,接着再次用5筛选,然后用11继续筛选……如此反复操作,直至过程结束,最终剩余的数字全为质数。这种方法被称为埃拉托斯特尼筛法,是一种经典且高效的寻找质数的算法。
63、 代码如下所示
64、 初始化数据
65、 }
66、 循环次数为 N 的平方根
67、 }
68、 循环执行 N/i 次,筛选出能被 i 整除的数值。
69、 }
70、 }
71、 输出计算次数:加上变量 count 的值。
72、 }
73、 }
74、 }
75、 }
76、 }