学习。
1、 将任意方阵分解为下三角矩阵、上三角矩阵与置换矩阵的乘积,称为LU分解或高斯消去法。
2、 L 是单位对角线的下三角矩阵的置换形式,U 为上三角矩阵。
3、 因理论与计算需要,矩阵必须进行置换操作。
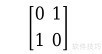
4、 某些矩阵无法通过三角矩阵相乘得到,即使不交换其行。
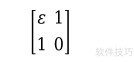
5、 当ε较小时,三角矩阵分解的因子元素可能变得很大,从而放大误差。因此,即使不必须进行行交换,适当置换仍被推荐。采用部分主元消元法可有效控制,使L矩阵的元素绝对值不超过1,同时保证U矩阵的元素大小不超出原矩阵A的元素范围,从而提升数值稳定性。
6、 例如:
7、 对A进行LU分解可得下三角与上三角矩阵。
8、 快速求解线性方程组可用达式
9、 利用LU分解,可依据特定公式计算行列式与逆矩阵。
10、 和
11、 可通过det(A) = prod(diag(U))求行列式,但结果符号可能与实际相反。


