许多朋友对dx的计算方法不太了解,本文将详细介绍dx的具体计算步骤与技巧,帮助大家轻松掌握。
1、 首先要理解dx的含义,在数学中,dx表示微分,是微分的一种标准表达形式。
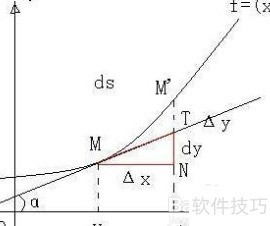
2、 微分是数学中的一个概念,对于函数B=f(A),当A中变量dx趋近于某点时,函数在该点的极限即为微分,其核心思想在于将变化量无限细分,体现函数局部的线性近似特性。
3、 微分是微积分中的基本概念,表示函数变量变化的线性主部。当自变量x的增量Δx被记为dx时,有dx = Δx。对于函数y = f(x),其微分记为dy = f(x)dx。由于函数因变量的微分与自变量微分之比恰好等于该函数的导数,因此导数也被称为微商,体现了变化率的本质。
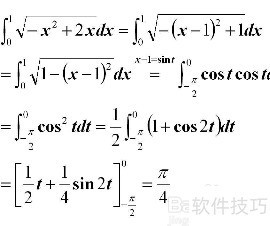
4、 函数 f(x) = 2x? + 5x + 1 的导数为 4x + 5,即对该多项式进行求导运算所得结果。

5、 导数的符号可写作(dy)/(dx)=f′(x),这不仅代表导数本身,也可理解为两个微分之比。当自变量的增量△x视为dx时,即自变量的增量等于其微分,于是有dy=f′(x)dx,体现出微分之间的关系。

6、 理解微分的基本含义
7、 掌握微分计算方法
8、 掌握求导方法


