数学期望是概率论和统计学中的基本概念,表示每次试验可能结果与其概率的乘积之和,反映随机变量平均值的大小,是重要数学特征之一。
1、 数学期望的简单计算公式如下。
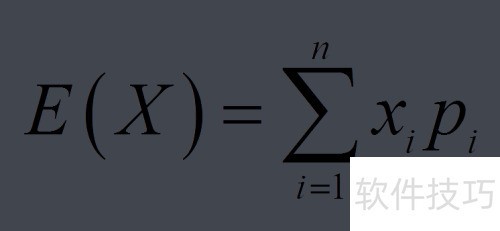
2、 离散型随机变量的数学期望公式及其定义。

3、 每件事的发生都有概率, 若要计算最终结果, 就需要我们仔细分析事件的特性。
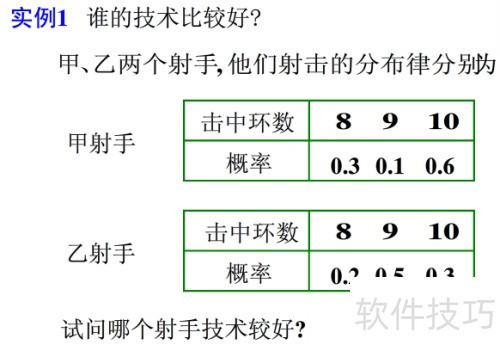
4、 其次,要掌握每件事发生的概率,将结果与概率相乘,再累加所有值,便能得到该事件的期望结果。

5、 通常,我们将事件发生的情况记为X,其概率记为P,所有事件的概率之和为1,这便是离散型随机变量的概念。

6、 连续型随机变量数学期望的计算公式如下。

7、 连续型随机变量呈指数分布,考试中概率低于离散型,建议简单了解即可。




















