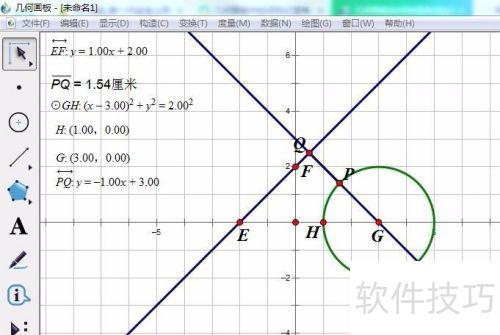
圆上动点到直线距离的最值问题是高考常见题型,重点考察转化化归和数形结合的思想方法。在教学过程中,如何通过直观的方式让学生理解并掌握这一知识点,引导他们用数学思维观察、分析和表达世界,具有重要意义。实际教学中,我们利用几何画板解决此类问题,不仅形象直观,还能即时验证结果,极大提升了学习效率。以下分享具体经验。
1、 以(3,0)为圆心,2为半径作圆。
2、 画出直线y=x+2
3、 圆上动点P向直线作垂线,垂足为Q。
4、 量一下PQ有多长。
5、 所示,5月28日
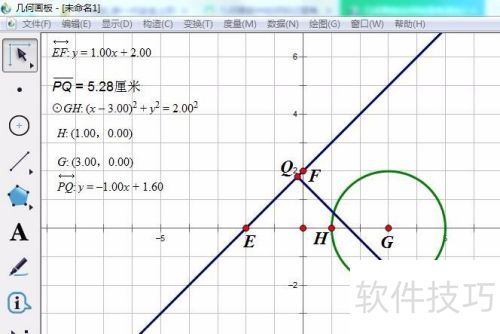
6、 拖动点P沿圆周移动。
7、 Q点随之移动
8、 我们发现PQ长度时而增大,时而减小。

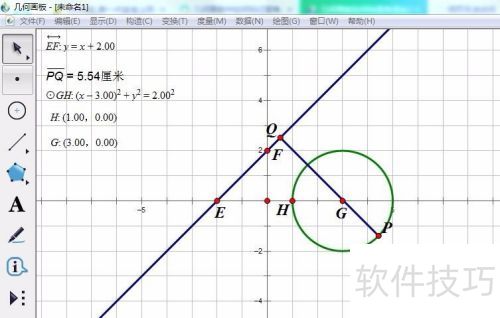
9、 所示,当P点处于图中状态时,我们发现
10、 峰值质量因子PQ=5.54,达到最大值。
11、 此时,PQ经过圆心,且圆心为线段PQ的内分点。
12、 我们得出一种猜测
13、 当PQ过圆心且圆心为线段PQ的内分点时,PQ长度达最大值5.54。
14、 验证假设是否成立
15、 过圆心G作直线y=x+2的垂线,得出该垂线方程为y=-x+3,标记为PQ。
16、 恰好经过P点,因此猜想得以验证。

17、 参照第五步,提出猜想:
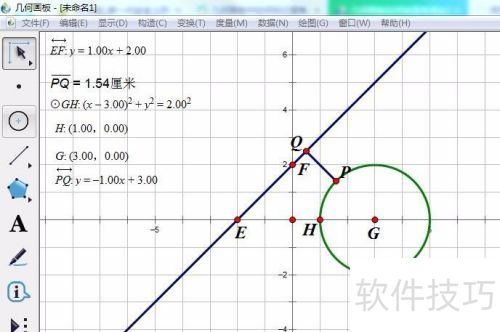
18、 Q=1.54是最大值。
19、 此时,PQ经过圆心,且圆心为线段PQ的外部分割点。
20、 我们获得一个猜想
21、 PQ过圆心,当圆心为线段PQ的外分点时,PQ长达到最小值1.54。
22、 检验假设:
23、 过圆心G作直线y=x+2的垂线,求得该垂线方程为y=-x+3,记为PQ。
24、 恰好经过P点,因此猜想成立。