本系列文章旨在讲解高等数学的基础知识,注重学习方法的引导。对于初学者可能难以理解的内容,会详加解释,并尽可能与高中数学内容衔接。一些高中数学中较少涉及但高数需要用到的知识点(如极坐标),会在用到时补充说明。同时,适当简化了部分难度较大或在高等数学中非核心的内容,例如省略了用ε-δ语言证明极限的过程,以及教材中某些定理的复杂证明,以帮助读者更好地掌握核心概念。
1、 中值定理在实际应用中的重要意义。
2、 微分中值定理是微积分的重要基石,其理论价值将在后续学习中逐步显现。然而,由于该定理仅能确保中值存在而无法明确求解,初学者常对其实际应用产生疑虑。接下来,我们将通过介绍柯西中值定理的一个关键应用——洛必达法则,展示其在解决未定式极限问题中的重要作用。
3、 求极限是高等数学中首个重要的计算内容,贯穿始终。需要强调的是,极限计算从来都不简单(回想第一章练习题)。直到学习洛必达法则后,这种情况才在本质上得到改观。
4、 从柯西中值定理出发,可推导洛必达法则,这是其证明的核心思路。

5、 情形一:x趋近a时的洛必达法则。
6、 定理一说明:仅未定式适用洛必达法则,且该法则可连续使用。请注意这两个关键条件。

7、 x趋近于a情况下的几个简单例题。

8、 情形二:当x趋近于无穷大时,适用洛必达法则。

9、 几个关于x趋近于无穷的简单例题。

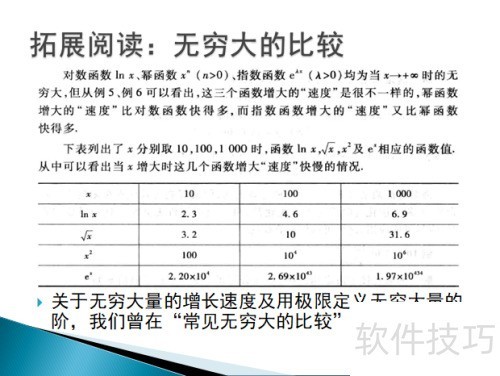
10、 延伸阅读:无穷大的对比分析。
11、 无穷大量的增长速率与阶的极限定义,详见下文介绍。
12、 高等数学入门:常见无穷大比较