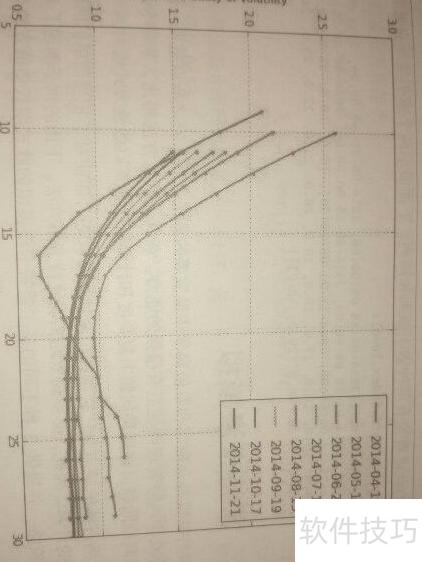
隐含波动率是根据市场上已知的期权实际价格反向推导得出的数值。由于现实中的期权价格(F)往往与理论模型存在差异,因此F由市场竞价形成,而与其对应的波动率则是隐含的。通过迭代等方法可求出该波动率,即为隐含波动率。在BS模型中,给定标的资产价格、波动率、到期时间、行权价和无风险利率可计算出理论期权价格,若将实际市场价格代入反推,则得到的波动率便是隐含波动率。
1、 运用Black-Scholes模型计算期权理论价格的方法
2、 现价 s
3、 执行价格k
4、 上述函数仅为计算隐含波动率的基础部分,还需引入基于VSTOXX指数的欧式看涨期权报价,并编写生成隐含波动率的程序代码,接下来将通过IPython环境逐步实现这一过程,完成整体计算与分析任务。
5、 例如将参考日期设为t=0。
6、 指数收盘价为7.6639
7、 假设无风险短期年利率为1%。
8、 如此便可善用
9、 输出期权价格,保留四位小数,通过BSM模型计算看涨期权价值,参数包括标的资产价格、行权价、到期时间、无风险利率和波动率。
10、 换个说法
11、 当前现货价格
12、 行权价格 strike
13、 到期时间
14、 无风险利率为r
15、 波动率,衡量价格变动幅度
16、 后续将遍历所有到期日并绘图展示。