Maple是一款功能强大的符号计算系统,广泛应用于数学和科学领域,被誉为数学家的软件。
1、 启动Maple软件,新建工作表模式,按照图示操作。

2、 求解命令:
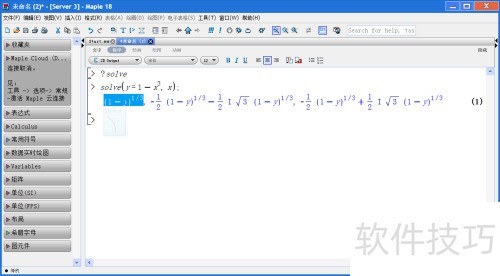
3、 利用Maple的solve命令求解,示例:求函数y=1-x^3的反函数表达式。
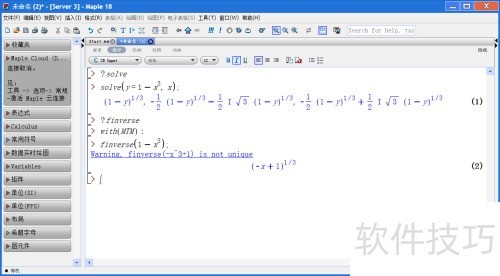
4、 可以将其视为一个方程或隐函数,求解x即可。下面得到三个解,其中有两个是复数根(在高中阶段通常只关注实数解)。实数范围内的解为蓝色部分,表达式为x=(1-y)^(1/3),需要注意定义域和值域的范围。
5、 查找满足条件的函数值
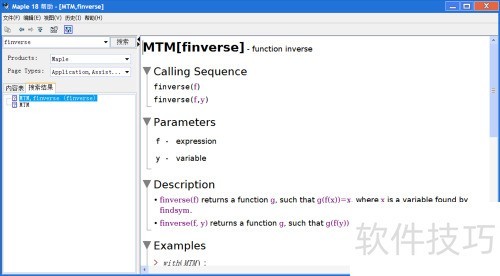
6、 此外,Maple的MTM包里有finverse命令,该命令有两种调用方式:
7、 finverse(f) 返回函数 g,满足 g(f(x))=x,其中 x 为默认变量。
8、 finverse(f, y) 返回函数 g,满足 g(f(y))=y,即以 y 为自变量求解对应的反函数关系。
9、 仍以上例:y=1-x?,即f=1-x?,因x为自变量,故采用第一种形式即可。
10、 (注意:MTM包需自行引入,使用 with(MTM) 即可。)
11、 结果所示,警告提示反函数可能不唯一(因为用 solve 求解时存在复数解,但我们只需实数解,因此可忽略警告)。所得反函数为 g(x) = (1-x)^(1/3),此时的 x 并非原函数 f(x) = y = 1-x^3 中的 x,而是对应原函数中的 y,这一点需特别留意。